Informatika ☆ 2023-24 | proiektua: otsaila 2024

2024(e)ko otsailaren 28(a), asteazkena

15. Ariketa: azpiprogramak (III)

ZER DAKIDAN:
Ariketa bati dagokion kodifikazioa programa monolitiko batean idazteko gai naiz eta programa moduluetan zatitzeko gai naiz.

ZER IKASIKO DUDAN:
Programa bat zatitzen ikasiko dut moduluak sortuz, modulu horiek azpiprogramak deitzen dira eta bi motatakoak izan daitezke: funtzioak edo prozedurak. Ikas dezagun noiz erabili funtzioa eta noiz prozedura.

ESKATZEN DEN PROGRAMA

Zirkunzentro: Poligono batera zirkunskribatua dagoen zirkunferentziaren zentroa. Poligonoa triangelua bada, hiru erdibitzaileek elkar ebakitzen duten puntua da zirkunzentroa.

Triangeluaren zirkunzentroa eta zirkunferentzia zirkunskribatua

Triangeluaren zirkunzentroa non kokatzen den triangeluak dituen angeluen araberakoa da. Horrela, triangelu angeluzuzena bada zirkunzentroa triangeluaren hipotenusaren gainean kokatzen da, baina angelu kamutsa badu zirkunzentroa triangelutik kanpo geratzen da eta triangeluaren barruan angelu zorrotzak baditu.

Zirkunzentroaren kokapena triangeluarekiko

TRIANGELUAREN HIRU ERPINAK:

A puntua eta B puntua segmentu horizontal batean daude
A puntua eta B puntua ez dira bat
C puntua ez dago AB segmentu horizontalean
AC segmentua ez da bertikala
BC segmentua ez da bertikala

Goiko baldintzak betetzen dituzten triangeluaren hiru erpinen rAx, rAy, rBx, rBy, rCx eta rCy koordenatuak datutzat emanik, zirkunferentzia zirkunskribatuaren rR erradioa kalkulatu ondoko formula erabiliz:

Non a, b eta c triangeluaren aldeak diren eta S azalera den

Horregatik, triangeluaren rA, rB eta rC aldeen luzerak eta rS azalera kalkulatu behar dira. Aldeak lortzeko pitagoras aplikatuko dugu funtzio baten bitartez, eta S azalera eskuratzeko ondoko formula barneratzen duen funtzioa idatziko dugu:

S = 1/2(rAx·rBy + rBx·rCy + rCx·rAy - rCx·rBy - rBx·rAy - rAx·rCy)

Zirkunferentziaren erradioa zehaztu ondoren, zirkunferentziaren Z zentroa kalkulatuko dugu, hots, rZx eta rZy koordenatuak kalkulatuko ditugu. Horretarako, komenigarria izango da 3. astea | triangeluaren azalera ariketa birpasatzea, non zuzen bat adierazteko malda-desplazamendua bikotea erabiltzen den. Dagokigun ariketa honetan AC eta BC segmentuen maldak eta desplazamenduak eskuratzen dira, eta horiei esker AC eta BC segmentu biren ebakidura (rZx, rZy) puntuaren koordenatuak kalkulatzen dira.

Irudiko P puntua, ariketa honetan bilatzen den Z zentroa litzateke

Zirkunferentziaren erradioa eta zentroa ezagunak direla, frogatzerik dago zirkunferentzia horrek triangelua zirkunskribatzen duen, horretarako hiru erpinek zirkunferentziaren formula bete beharko dute. Hauxe da ariketaren programa nagusia eta azpiprogramen goiburuak:

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

{ 15. ariketa: A, B eta C erpinez triangelua definitu (6 koordenatu). }
 
{     AB aldea horizontala izango da eta ABC triangeluari dagokion    }
{     zirkunferentzia zirkunskribatuaren R erradioa kalkulatu.        }
{     ABC triangeluari dagokion zirkunferentzia zirkunskribatuaren Z  }
{     zentroaren bi koordenatuak Zx eta Zy kalkulatu.                 }
 
{     Datuak hiru erpinen koordenatuak dira eta prozedura batean      }
{     hartzen dira, adibidez: (0.0, 0.0), (4.0, 0.0) eta (2.0, 2.0)   }
       
program Ariketa__15 ;
 
{ Eskatzen diren azpiprogramak hemen idatzi:           }
 
{   - ErpinakEskuratu                  prozedura (irteerako 6 parametro)    }
{   - fnrAldeaLortu                     funtzioa (sarrerako 4 parametro)    }
{   - fnrAzaleraLortu                   funtzioa (sarrerako 6 parametro)    }
{   - fnrErradioaLortu                  funtzioa (sarrerako 4 parametro)    }
{   - fnrZuzenarenMalda                 funtzioa (sarrerako 4 parametro)    }
{   - SegmentuarenErdia                prozedura (sarrerako 4 parametro,    }
{                                                 irteerako 2 parametro)    }
{   - ZentroaKalkulatu                 prozedura (sarrerako 4 parametro,    }
{                                                 irteerako 2 parametro)    }
{   - fnboErpinaZirkunferentzianDago    funtzioa (sarrerako 5 parametro)    }
 
{ ---------------------------Programaren Nagusia--------------------------- }   
                              
var
   rAx, rAy, rBx, rBy, rCx, rCy, rZx, rZy : real ;        { koordenatuak }
   rErdiaACx, rErdiaACy, rErdiaBCx, rErdiaBCy  : real ;   { koordenatuak }
   rA, rB, rC, rR : real ;                                { distantziak }
   rS : real ;                                            { azalera }
   rMaldaAC, rPerpendikularraAC : real ;                  { maldak }
   rMaldaBC, rPerpendikularraBC : real ;                  { maldak }
   rDesplazamendu1 : real ;                               { distantzia }
   rDesplazamendu2 : real ;                               { distantzia }
begin
   writeln ;
   writeln ;
   writeln ;
   writeln ;
    
   { triangeluaren hiru erpinak irakurri }
   ErpinakEskuratu(rAx, rAy, rBx, rBy, rCx, rCy) ;
    
   writeln ; 
    
   { triangeluaren hiru aldeak lortu }
   rA := fnrAldeaLortu(rBx, rBy, rCx, rCy) ;   { BC segmentuaren luzera lortu }
   rB := fnrAldeaLortu(rAx, rAy, rCx, rCy) ;   { AC segmentuaren luzera lortu }
   rC := fnrAldeaLortu(rAx, rAy, rBx, rBy) ;   { AB segmentuaren luzera lortu }
       
   writeln('   BC aldea, rA = ', rA:0:2, ' m') ;   { BC aldearen luzera erakutsi }
   writeln('   AC aldea, rB = ', rB:0:2, ' m') ;   { AC aldearen luzera erakutsi }
   writeln('   AB aldea, rC = ', rC:0:2, ' m') ;   { AB aldearen luzera erakutsi }
    
   { triangeluaren azalera kalkulatu erpinak ezagunak izatean }
   rS := fnrAzaleraLortu(rAx, rAy, rBx, rBy, rCx, rCy) ;
     
   writeln('   rS azal. = ', rS:0:3, ' m^2') ;
   writeln ;
    
   { erradioa kalkulatzeko formula: (rA·rB·rC)/(4·rS) }
   rR := fnrErradioaLortu(rA, rB, rC, rS) ; 
 
   writeln('   rR erra. = ', rR:0:3, ' m') ;
   writeln ;   
    
   { AC perpendikularraren malda }
   rMaldaAC := fnrZuzenarenMalda(rAx, rAy, rCx, rCy) ;
   writeln('   AC malda = ', rMaldaAC:0:2) ;
   rPerpendikularraAC := -(1/rMaldaAC) ;
   writeln('   AC perp. = ', rPerpendikularraAC:0:2) ;
    
   { AC perpendikularren zuzenak duen desplazamendua }
   SegmentuarenErdia(rAx, rAy, rCx, rCy, rErdiaACx, rErdiaACy) ;                 
   writeln('   AC erdia = (', rErdiaACx:0:2, ', ', rErdiaACy:0:2, ')') ;     
   rDesplazamendu1 := rErdiaACy + rErdiaACx/rMaldaAC ;
   writeln('   Desplaz1 = ', rDesplazamendu1:0:2, ' m') ;
   writeln ;
 
   { BC perpendikularraren malda }
   rMaldaBC := fnrZuzenarenMalda(rBx, rBy, rCx, rCy) ;
   writeln('   BC malda = ', rMaldaBC:0:2) ;
   rPerpendikularraBC := -(1/rMaldaBC) ;
   writeln('   BC perp. = ', rPerpendikularraBC:0:2) ;
    
   { BC perpendikularren zuzenak duen desplazamendua }
   SegmentuarenErdia(rBx, rBy, rCx, rCy, rErdiaBCx, rErdiaBCy) ;       
   writeln('   BC erdia = (', rErdiaBCx:0:2, ', ', rErdiaBCy:0:2, ')') ;
   rDesplazamendu2 := rErdiaBCy + rErdiaBCx/rMaldaBC ;
   writeln('   Desplaz2 = ', rDesplazamendu2:0:2, ' m') ;
   writeln ;   
    
   { Zentroa bi zuzen perpendikularren arteko ebakidura izango da }
   { Zuzen z1:   m1 = rPerpendikularraAC | d1 = rDesplazamendu1   }
   { Zuzen z2:   m2 = rPerpendikularraBC | d2 = rDesplazamendu2   }
 
   { Zuzen z1:   rZy = m1·rZx + d1      }
   { Zuzen z2:   rZy = m2·rZx + d2      }
    
   { m1·rZx + d1 = m2·rZx + d2  ==>  rZx = (d1 - d2) / (-m1 + m2)          }
   {         rZy = m1·rZx + d1  ==>  rZy = m1·(d1 - d2) / (-m1 + m2) + d1  }
    
   { rZx = (d1 - d2) / (-m1 + m2)       }
   { rZy = (m2·d1 - m1·d2) / (-m1 + m2) }
    
   ZentroaKalkulatu(rPerpendikularraAC, rPerpendikularraBC, rDesplazamendu1, rDesplazamendu2, rZx, rZy) ;
   
   writeln('   Z zentr. = (', rZx:0:2, ', ', rZy:0:2, ')') ;
   writeln ;
   writeln ;
         
   writeln('   (x - rZx)^2 + (y - rZy)^2 - rR^2  <  0.000001') ;
    
   if fnboErpinaZirkunferentzianDago(rZx, rZy, rR, rAx, rAy) then
      writeln('   (', rAx:0:2, ', ', rAy:0:2, ') erpina zirkunferentzian dago')
   else
      writeln('   Errorea A erpinean') ;
   if fnboErpinaZirkunferentzianDago(rZx, rZy, rR, rBx, rBy) then
      writeln('   (', rBx:0:2, ', ', rBy:0:2, ') erpina zirkunferentzian dago')
   else
      writeln('   Errorea B erpinean') ;
   if fnboErpinaZirkunferentzianDago(rZx, rZy, rR, rCx, rCy) then
      writeln('   (', rCx:0:2, ', ', rCy:0:2, ') erpina zirkunferentzian dago')
   else
      writeln('   Errorea C erpinean') ;
          
   writeln ;
   readln ;
end.            { Programaren amaiera }

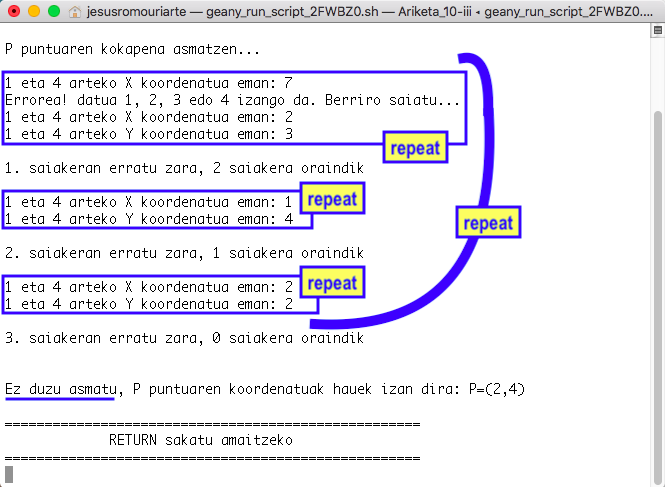
Programaren balizko exekuzio bat hurrrengo irudian erakusten da:

Emaitza laster...

14. Ariketa: azpiprogramak (II)

ZER DAKIDAN:
Menu bat programa batean nola egiten den badakit.

ZER IKASIKO DUDAN:
Menu bat funtzio batean kodetu eta programa nagusitik deiak egiten ikasiko dut.

Ariketa hauek gogora ekarri eta ariketa guztiak programa bakar batean bildu:

3. Ariketa: datuak teklatuz irakurri (menuaren A aukera)
8. Ariketa: errepikapen kopuru ezaguna (menuaren B aukera)
5. Ariketa: zenbaki errealetik kopuru osora (II) (menuaren C eta D aukerak)

Programa berria modulutan antolatzeko funtzioak eta prozedurak erabili. Programa berriaren exekuzioa gidatzeko menu honetaz baliatu:

====================================Menua====================================
  A  Mendi baten altuera emanik zeruertzaren distantzia lortu
  B  Dado bat 5 aldiz jaurti ondoren balio minimoa eta maximoa pantailaratu
  C  Koordenatuak formatuz aldatu: Hirurogeitatarretik dezimalera
  D  Koordenatuak formatuz aldatu: Dezimaletik hirurogeitatarrera
    
  I  Programatik irten
=============================================================================

Baina, menu horren aukeraren hautapena funtzio batean egin dadila. Hau da, programa nagusian fncMenua funzioari deia egingo zaio, eta fncMenua funtzio barruan aukeren deskribapenak erakutsi ondoren, erabiltzailaren hautapena teklatuz jasoko da eta balio hori funtzioak programa nagusiari itzuliko dio.

Programa nagusiak itxura hau izango du:

begin
  repeat
     cAukera := fncMenua ;
 
     case cAukera of
        'A': begin
                (* A  Mendi baten altuera eman eta zeruertzaren distantzia lortu *)
             end ;
        'B': begin
                (* B  Dado bat 5 aldiz jaurti ondoren balio minimoa eta maximoa pantailaratu *)
             end ;
        'C': begin
                (* C  Koordenatuak formatuz aldatu: Hirurogeitatarretik dezimalera *)
             end ;
        'D': begin
                (* D  Koordenatuak formatuz aldatu: Dezimaletik hirurogeitatarrera *)
             end ;
     end ;
 
     if cAukera <> 'I' then
     begin
        cItxaron := readkey ;
        writeln(cItxaron) ;
     end ;
 
     clrscr ;
  until cAukera = 'I' ;
end.

Hona hemen programaren balizko exekuzio bat:

Ariketa__14.pas

13. Ariketa: azpiprogramak (I)

Leonardo Pisano (Pisa, Italia, 1170-1250), Leonardo Bonacci, Leonardo Fibonacci edo Fibonacci moduan ezaguna, Italiar matematikaria izan zen, Erdi Aroko ezagunetarikoa. Ezaguna da batez ere bi aurkikuntzengatik:

Hindu-arabiar zenbaki sistema Europan sartu zuen eta berau erabiltzeko bideak jarri zituen XIII. mendeko "Liber Abaci" liburuaren bitartez
Fibonacciren zenbakiak deskribatu zituen liburu berean, nahiz eta berak ez zituen aurkitu baizik eta adibide moduan jarri

Leonardo Pisano, Fibonacci, ezagutzeko hemen duzu artikulu bat Fibonacci, el matemático que se puso a contar conejos y descubrió la secuencia divina.

Fibonacciren sekuentziako lehen zenbakia 0 da, Fibonacci-ren bigarren zenbakia 1 da, eta hirugarren zenbakia lortzeko aurreko biak batuko dira, horregatik Fibonacciren hirugarren zenbakia 1 da, laugarren zenbakia 2 izango da, bosgarrena 3, ...

Beraz, Fibonacciren sekuentzia honako hau da:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...

Fibonacciren zenbakiak grafikoki adieraztean honako blokeen sorta eta espirala lortzen dira:

Fibonacciren sekuentziako bi zenbaki hartuz eta zatiketa eginez, urrezko zenbakia edo jainkozko proportzioa edo urrezko proportzioa edo zerutiar zenbakia lortzen da:

Fibonacciren sekuentzia sarritan agertzen da naturan. Izan ere, naturan hazkundea gertatzen denean Fibonacciren sekuentziaren arabera ematen da:

Eskatzen den programa (prozedura bat eta funtzio bat)

Programa bakarra izan arren programak bi zati izango ditu. Lehen zatian prozedura bati dei egingo zaio eta programaren bigarren zatian funtzio bati dei egingo zaio.

Programaren prozedura eta programaren funtzioa jarraian deskribatzen dira eta bakoitzaren kode gehiena ematen da. Ikaslearen lana da kodeak bukatzea eta programaren emaitzak ulertzea.

Lehen zatia. Fibonacciren sekuentzia osatuko duten zenbakien iZenbat kopurua teklatuz irakurri programa nagusian eta prozedura batek ondoko taularen pantailaraketa egin dezala FOR-DO egitura bat erabiliz, FibonaccirenSekuentziaPantailaratu izeneko prozeduraren barruan errepikatzen den prozesua hau delarik:

procedure FibonaccirenSekuentziaPantailaratu(iZenbat: integer) ;
 
   ...
 
begin { prozeduraren kodea hemen hasten da }
 
   ...
    
   for k:=3 to iZenbat do
   begin
      iFibo3 := iFibo1 + iFibo2 ;
      iIndizea := iIndizea + 1 ;
      writeln(iIndizea:15, iFibo3:15, 1.0*iFibo3/iFibo2:25:7) ;
    
      iFibo1 := iFibo2 ;
      iFibo2 := iFibo3 ;
   end ; 
 
   ...
    
end ; { prozeduraren kodea hemen amaitzen da }     

Programaren lehen zatiko irteera bat hau izan daiteke:

Bigarren zatia. Prozesu errepikakor bat izango da eta bertatik irteteko b edo B erantzun beharko da, bestela programa nagusian iMuga teklatuz irakurriko da eta funtzio batek kalkulatuko du 0-tik hasita zenbat Fibonacciren zenbaki dauden. Horretarako, WHILE-DO egitura bat erabiliko da, funtzio barruko prozesu errepikakorra hauxe da, non funtzioak itzuli behar duen emaitza iFiboKopuru den eta arrazoi horregatik balio hori kanporatu behar du fniFibonacciZenbakienKopuruaKalkulatu izeneko funtzioak:

function fniFibonacciZenbakienKopuruaKalkulatu(iMuga: integer): integer ;
 
   ...
 
begin { funtzioaren kodea hemen hasten da }
 
   ...
    
   iFibo1 := 0 ;
   iFibo2 := 1 ;
   iFibo3 := iFibo1 + iFibo2 ;
 
   while iFibo3 <= iMuga do
   begin
      iFibo1 := iFibo2 ;
      iFibo2 := iFibo3 ;
      iFibo3 := iFibo1 + iFibo2 ;
      iFiboKopuru := iFiboKopuru + 1 ;
   end ;
 
   fniFibonacciZenbakienKopuruaKalkulatu := iFiboKopuru ;
end ; { funtzioaren kodea hemen amaitzen da }

Programaren bigarren zatiko irteera bat hau izan daiteke:

Ariketa__13.pas

12. Ariketa: hainbat aukeren menu bat

ZER DAKIDAN:
CASE-OF baldintzazko egitura ikasi nuen aukera anitzak antolatzeko.

ZER IKASIKO DUDAN:
Menu bat programa batean nola egiten den ikasiko dut, erabiltzaileak gogoko duen hautapena CHAR datu-motako aldagai batean irakurriko dut. Bide batez clrscr prozedura ikasiko dut ere.

6. Ariketa: aukera anitzen arteko hautapena artikulua gogora ekarriz, programaren fluxua bideratzeko CASE-OF agindua erabilten da aukerak hiru edo gehiago direnean.

Jarraian erakusten den menua programa nagusian kokaturik dago, baina jakin ezazu hori horrela ez dela egingo behin azpiprogramen kontzeptua gureganatuko dugunetik aurrera.

Algoritmoa:

Programa osoa prozesu errepikakor bat da, eta errepikapenak mozteko menuaren aukera egokia hautatu behar da (adibidean A balioa)
Begiztaren iterazio bakoitzeko, pantaila garbitu clrscr prozeduraren bitartez eta bost aukeren deskribapenak erakutsi
Begiztaren iterazio bakoitzeko, CHAR datu-motako cAukera aldagaiari balioa teklatuz eman era kontrolatuan (teklatuaren karaktere bat irakurtzeko readkey funtzioa oso egokia da)
Irakurri den karaktere horren arabera CASE-OF egiturak kudeatuko du programaren fluxoa eta aukera horri dagozkion kalkuluak burutuko dira
Begiztaren iterazio bakoitzeko, programaren exekuzioa gelditu readkey funtzioaren bitartez tekla bat sakatu arte, horrela kalkuluen emaitzak ikusi ahal izango dira

clrscr prozedura estandarra eta readkey funtzio estandarra erabili ahal izateko, beharrezkoa da crt unitatea dekalaratzea uses blokean.

ESKATZEN DEN PROGRAMA

Programa honek goiko algoritmoa aplikatzen du:

{ Aukera modu kontrolatuan irakurtzen delako case-OF aginduak ez du else kasurik behar }
program Ariketa_12 ;
uses
   crt ;   (* clrscr prozedura eta readkey funtzioa erabiltzeko *)
var
   cAukera, cItxoin : char ;
   rEragigai1, rEragigai2 : real ;
begin
   repeat
      clrscr ;
      writeln ('============Menua============') ;
      writeln ('  +   Batura lortzeko') ;
      writeln ('  -   Kendura lortzeko') ;
      writeln ('  *   Biderkadura lortzeko') ;
      writeln ('  /   Zatiketa burutzeko') ;
      writeln ('  A   Programa amaitu') ;
      writeln ('=============================') ;
      repeat
         write ('          Zure aukera: ') ;
         cAukera := readkey ;
         cAukera := upcase(cAukera) ;
         writeln (cAukera) ;    (* readkey funtzioak ez du irakurritako tekla erakusten *)
      until (cAukera ='+') or (cAukera ='-') or (cAukera ='*') or (cAukera ='X') or (cAukera ='/') or (cAukera ='A') ;
      writeln ;
      case cAukera of
         '+' : begin
                  write ('Zenbaki errealekin lan eginez, lehenengo batugaiaren balioa eman: ') ;
                  readln (rEragigai1) ;
                  write ('Zenbaki errealekin lan eginez, bigarren batugigaiaren balioa eman: ') ;
                  readln (rEragigai2) ;
                  writeln (rEragigai1:0:2, ' + ', rEragigai2:0:2, ' = ', rEragigai1+rEragigai2:0:2) ;
               end ;
         '-' : begin
                  write ('Zenbaki errealekin lan eginez, kenkizunaaren balioa eman: ') ;
                  readln (rEragigai1) ;
                  write ('Zenbaki errealekin lan eginez, kentzailearen balioa eman: ') ;
                  readln (rEragigai2) ;
                  writeln (rEragigai1:0:2, ' - ', rEragigai2:0:2, ' = ', rEragigai1-rEragigai2:0:2) ;
               end ;
         '*','X' : begin
                      write ('Zenbaki errealekin lan eginez, lehenengo biderkagaiaren balioa eman: ') ;
                      readln (rEragigai1) ;
                      write ('Zenbaki errealekin lan eginez, bigarren biderkagaiaren balioa eman: ') ;
                      readln (rEragigai2) ;
                      writeln (rEragigai1:0:2, ' * ', rEragigai2:0:2, ' = ', rEragigai1*rEragigai2:0:2) ;
                   end ;
         '/' : begin
                  write ('Zenbaki errealekin lan eginez, zatikizunaren balioa eman: ') ;
                  readln (rEragigai1) ;
                  repeat
                     write ('Zenbaki errealekin lan eginez, zatitzailearen balioa eman: ') ;
                     readln (rEragigai2) ;
                  until rEragigai2 <> 0.0 ;
                  writeln (rEragigai1:0:2, ' / ', rEragigai2:0:2, ' = ', rEragigai1/rEragigai2:0:2) ;
               end ;
         'A' : begin
                  writeln ('Programatik irtetera goaz!') ;
               end
      end ;
  
      cItxoin := readkey ;         (* emaitzak ikusi ahal izateko itxaron *)
      writeln(cItxoin) ;           (* konpilazio abisua kentzeko *)
   until cAukera='A' ;
end. 

Ariketa__12.pas

11. Ariketa: bi letren arteko distantzia

ZER DAKIDAN:
Funtzio batek sarreraren bat hartzen du eta emaitza bakar bat itzultzen du. Dagoeneko zenbakien funtzio estandarrak erabili ditut.

ZER IKASIKO DUDAN:
CHAR datu-mota, eta CHAR datu-motarekin lotutako funtzio estandar batzuk:

upcase eta lowercase
chr eta ord
pred eta succ
readkey

Bide batez, hainbat zenbakiren artean minimoa zein den zehazten ikasiko dut.

A eta Z arteko letra maiuskula bat gure erreferentzia da. Prozesu errepikakor bat hasi eta teklatuaren bitartez letra bat irakurri, ereferentziaren eta irakurriko letraren arteko distantzia (zenbaki bat) kalkulatu balio minimoa gordez. Prozesu errepikakorretik irteteko erreferentzia den letra teklatuz irakurri. Programa amaitu aurretik pantailaratu letrarik hurbilena eta bere distantzia erreferentziarekiko.

Algoritmoa:

Erreferentzia teklatutik irakurri, cErreferentzia aldagaiari balioa eman (jakinik letra maiuskula bat izan beharko dela)
Hasieraketak. Bi izan daitezke, alde batetik distantzia minimoa gordeko duen iMinimoa zenbaki osoa (minimoa bilatzen ari garelako hasieran kopurua handi bat jarri beharko da); bigarren hasieraketa letrarik hurbilena gordetzeko cHurbilena aldagaia izango da, baina aurreko aldagaiarekin lotuta dagoenez bere hasieraketa ez da derrigorrezkoa
Begiztaren iterazio bakoitzeko: cLetra aldagaiari balioa teklatuz eman, eta erreferentziarekiko iDistantzia aldagaiari distantzia kalkulatu ord funtzio estandarra aplikatuz, iDistantzia aldagaiaren balioa eta iMinimoa aldagaiaren balioa alderatu erabakiak hartzeko (emaitzak zehazteko, hots, minimoak zehazteko)
Prozesu errepikakorretik irten cErreferentzia aldagaiaren balioa eta cLetra aldagaiaren balioa bat bera denean, baina kontuz, irtetean haien arteko diztantzia 0 izango da eta horrek minimoaren kalkuluarengan eragina du
cLetra aldagaiaren balioa eta iMinimoa aldagaiaren balioa pantailaratu

ESKATZEN DEN PROGRAMA

Programa honek goiko algoritmoa aplikatzen du:

{ Erreferentzia bat emanik, letra sorta bateko letrarik hurbilena. }
program Ariketa_11 ;
uses
  crt ;
var
  cErreferentzia, cLetra, cItxoin, cHurbilena : char ;
  iDistantzia, iMinimoa : integer ;
begin
    clrscr ;
    repeat
       write('Erreferentzia izango den A..Z alfabetoko letra eman: ') ;
       readln(cErreferentzia) ;
    until (cErreferentzia >= 'A') and (cErreferentzia <= 'Z') ;
  
    writeln ;
    writeln('Orain prozesu errepikakor batean sartuko gara, begizta edo itzuli bakoitzean') ;
    writeln('letra majuskula bat sartuz eta erreferentziarekiko distantzia kalkulatuz.') ;
    writeln ;
  
    iMinimoa := ord('Z') - ord('A') + 1 ;   (* alfabetoaren maximoa baino 1 gehiago *)
    cHurbilena := cErreferentzia ;          (* hasieraketa hau ez da derrigorrezkoa *)
    repeat
       repeat
          write('A..Z alfabetoko letra eman (bukatzeko ', cErreferentzia, ' eman): ' ) ;
          readln(cLetra) ;
       until (cLetra >= 'A') and (cLetra <= 'Z') ;
  
       if cLetra <> cErreferentzia then
       begin
          iDistantzia := abs(ord(cErreferentzia) - ord (cLetra)) ;
          writeln(cLetra, ' eta ', cErreferentzia, ' arteko aldea ', iDistantzia, ' da') ;
          writeln ;
          if iDistantzia < iMinimoa then
          begin
             cHurbilena := cLetra ;
             iMinimoa := iDistantzia ;
          end ;
       end ;
    until cLetra = cErreferentzia ;
  
    writeln('Letrarik hurbilena: ', cHurbilena) ;
    writeln(cHurbilena, ' eta ', cErreferentzia, ' arteko aldea ', iMinimoa, ' da') ;
  
    cItxoin := readkey ;
    write(cItxoin) ;
end.

Ariketa__11.pas

2024(e)ko otsailaren 17(a), larunbata

10. Ariketa: errepikapen kopuru ezezaguna (II)

ZER DAKIDAN:
FOR-TO-DO kontrol-egitura errepikakorra erabiltzeko gai naiz.

ZER IKASIKO DUDAN:
WHILE-DO kontrol-egitura errepikakorra ikasiko dut, eta REPEAT-UNTIL kontrol-egitura errepikakorra birpasatuko dut. Bide batez, zenbaki errealekin = konparatzailea ez dela erabili behar ikasiko dut ere.

ESKATZEN DEN PROGRAMA (I)

Zenbaki osoekin lan eginez, berdintzaren = ikurra kopuru osoekin. Lehen koadranteko zati bat definituko dugu, adibidean 4x4 espazio bat mugatu da. Ondoren, programak P puntu baten iPx eta iPy koordenatuak ausaz aukeratuko ditu 4x4 espazio horren barruan. Programaren erabiltzaileak P puntuaren koordenatuak asmatu beharko ditu. Horretarako, teklatuaren bitartez iQx eta iQy koordenatuak irakurriko ditu eta konparaketa egin ondoren emaitza pantailaratuko da.

Hona hemen programaren balizko bi irteera, irteera batean P puntuaren koordenatuak asmatzea lortu da eta bestean ez:

Zenbakiak ausaz lortzeko, berreskuratu 7. Ariketa: zenbakien funtzio estandarrak izeneko artikulua eta bertako (I) eta (II) programak gogoratu.

ESKATZEN DEN PROGRAMA (II)

Zenbaki errealekin lan eginez, berdintzaren = ikurra zenbaki errealekin. Lehen koadranteko zati bat definituko dugu, adibidean (0.0, 0.0) eta (4.0, 4.0) puntuen arteko espazio karratua mugatu da. Ondoren, programak P puntu baten rPx eta rPy koordenatuak ausaz aukeratuko ditu espazio horren barruan. Programaren erabiltzaileak P puntuaren koordenatuak asmatu beharko ditu. Horretarako, teklatuaren bitartez rQx eta rQy koordenatuak irakurriko ditu eta konparaketa egin ondoren emaitza pantailaratuko da.

Hona hemen programa desegokiaren balizko irteera bat, ikusten denez P eta Q puntuen koordenatuak konparatzerakoan = eragilea aplikatzen da eta hori ez dago ondo:

Eta hona hemen programa zuzenaren balizko irteera bat, ikusten denez P eta Q puntuen koordenatuak konparatzerakoan prezisio edo doitasun bat aukeratu da eta = eragilea aplikatu beharrean < eragilea aplikatzen da:

ESKATZEN DEN PROGRAMA (III)

Zenbaki osoekin lan eginez, berdintzaren = ikurra kopuru osoekin. Goiko I programan bezala, baina kasu honetan programaren erabiltzaileak 3 saiakera edukiko ditu gehienez. Lehen saiakeran asmatzen ez badu, ez zaio emango inolako informaziorik P puntuari buruz baina bigarren saiakera bat onartuko zaio. Bigarren saiakeran asmatzen ez badu, ez zaio emango inolako informaziorik P puntuari buruz baina hirugarren eta azken saiakera bat onartuko zaio.

Hona hemen programaren balizko irteera bat, repeat-until nagusiak saiakerak kontrolatzen ditu eta bere barneko repeat-until egiturek koordenatuen balioztapena zaintzen dute. Adibide honetan, hiru saiakera agortu ondoren ez dira P puntuaren koordenatuak asmatu:

ESKATZEN DEN PROGRAMA (IV)

Zenbaki errealekin lan eginez, berdintzaren = ikurra zenbaki errealekin. Goiko II programan bezala, baina kasu honetan programaren erabiltzaileak 3 saiakera edukiko ditu gehienez. Lehen saiakeran asmatzen ez badu, ez zaio emango inolako informaziorik P puntuari buruz baina bigarren saiakera bat onartuko zaio. Bigarren saiakeran asmatzen ez badu, ez zaio emango inolako informaziorik P puntuari buruz baina hirugarren eta azken saiakera bat onartuko zaio.

Hona hemen programaren balizko irteera bat, while-do nagusiak saiakerak kontrolatzen ditu eta bere barneko repeat-until egiturek koordenatuen balioztapena zaintzen dute. Adibide honetan, hirugarren saiakeran P puntuaren koordenatuak asmatu dira. Nahiz eta P eta Q puntuen koordenatuak berdin-bedinak ez izan, bai betetzen dute hurbil daudela ezarritako 0.1 doitasunarekin:

9. Ariketa: errepikapen kopuru ezezaguna (I)

ZER DAKIDAN:
FOR-TO-DO kontrol-egitura errepikakorra erabiltzeko gai naiz.

ZER IKASIKO DUDAN:
REPEAT-UNTIL kontrol-egitura errepikakorra ikasiko dut.

ESKATZEN DEN PROGRAMA (I)

7. Ariketa: zenbakien funtzio estandarrak artikuluaren (III) eta (IV) programetan balio positiboak irakurri behar dira teklatuaren bitartez. Baina nola behartzen dugu programaren erabiltzailea balio positiboak sar ditzan?

Erantzuna ondoko programa honetan erakusten da:

{ Zenbaki positiboak teklatuaren bitartez irakurtzen. }
program Ariketa__09_I ;
    
var
   rZenbakia, rEmaitza: real ;    
begin
   writeln ;
   writeln ;
   writeln ;
    
   writeln('Kopuru positiboekin lan egingo da.') ;
   writeln ;
    
   repeat
      write('Zenbaki baten logaritmoa lortzeko, kopuru positiboa eman (5.2 adibidez): ') ;
      readln(rZenbakia) ;
      if rZenbakia <= 0.0 then
         writeln('Errorea! sarrerako datua 0.0 baino handiagoa izan behar da') ;
   until rZenbakia > 0.0 ;
    
   rEmaitza := ln(rZenbakia) ;   
    
   writeln ;
   writeln('ln(', rZenbakia:0:2, ') = ', rEmaitza:0:2) ;
            
   writeln ; 
   writeln('====================================================') ;
   writeln('             RETURN sakatu amaitzeko') ;
   writeln('====================================================') ;
   readln ;
end. 

ESKATZEN DEN PROGRAMA (II)

7. Ariketa: zenbakien funtzio estandarrak artikuluaren (II) programan bi mugen arteko balio erreal batekin lan egiten da. Konkretuki, auto baten abiadura adierazten duen zenbaki erreal bat behar da, eta bere balioa bi mugen artekoa izan beharko da: behemuga 27.8 km/h eta goimuga 104.5 km/h. Gauza bera denborarako, autoak behar duen denbora 0.8 segundo eta 2.0 segundo artekoa izango da.

Abiadura eta denbora emanik, distantzia kalkulatzen duen programa idatzi. Abiadura adierazten duen balioa teklatuaren bitartez irakurri (27.8 km/h eta 104.5 km/h arteko balioa). Denbora adierazten duen balioa teklatuaren bitartez irakurri (0.8 segundo eta 2.0 segundo arteko balioa). Distantzia metrotan kalkulatu eta pantailaratu.

2024(e)ko otsailaren 8(a), osteguna

8. Ariketa: errepikapen kopuru ezaguna

ZER DAKIDAN:
Zenbaki osoekin lan eginez, hiru zenbakiren batura kalkulatzeko gai naiz. Baina nola egin beharko litzateke lan bera, zenbakien kopurua exekuzio-denboran erabakitzen bada.

ZER IKASIKO DUDAN:
FOR-TO-DO kontrol-egitura errepikakorra ikasiko dut.

ESKATZEN DEN PROGRAMA (I)

7. Ariketa: zenbakien funtzio estandarrak artikuluaren (I) programatik abiatuta, dadoa hainbat aldiz jaurtiko dugu eta jaurtiketa guztien emaitzak aintzat harturik batezbesteko aritmetikoa kalkulatuko dugu. Urratsak hauek lirateke:

Programak jaurtiketen kopurua erabaki Random funtzioa erabiliz (adibidez, jaurtiketen kopuru minimoa 1 eta maximoa 15)
Prozesu errepikakor bat ireki jaurtiketak burutzeko, jaurtiketa bakoitzean metagailu bat inkrementatu
Prozesu errepikakorra burutzen den bitartean batezbesteko aritmetikoa kalkulatzen aritu eta prozesu errepikakorra amaitu ondoren batezbesteko aritmetikoa pantailaratu

ESKATZEN DEN PROGRAMA (II)

Zenbaki osoekin lan eginez, hainbat zenbaki teklatuaren bitartez irakurri ondoren, balio maximoa zein izan den eta datuen sekuentzian zenbatgarrena izan den zehaztu.

Lehenik, zenbat datu izango diren eskatuko zaio erabiltzaileari (gutxienez bi datu), beraz, iZenbakienKopurua aldagaian datuen kopurua gorderik daukagu (adibidez 7 datu izango direla). Ondoren, eta prozesu errepikakorra hasi aurretik, lehendabiziko datua irakurriko dugu iZenbakia aldagaian gordez, une honetan balio maximoa lehen hori da eta ondoko hau egin beharko da:

iMaximoa aldagaian gorde iZenbakia aldagaiaren edukia
iZenbatgarrena aldagaian gorde 1 maximoa lehen datua delako

Ondoren, prozesu errepikakorra hasi eta bertan ondoko egin:

Hurrengo datua irakurri iZenbakia aldagaiari balio berria emanez
iZenbakia aldagaiaren balioa eta iMaximoa aldagaiaren balioa alderatu, eta k itzuli bakoitzeko behar izanez gero aldaketa hauek burutu:

iMaximoa aldagaian gorde iZenbakia aldagaiaren edukia
iZenbatgarrena aldagaian gorde maximoa k. datu hori delako

Ariketa__08-i.pas
Ariketa__08-ii.pas

7. Ariketa: zenbakien funtzio estandarrak

ZER DAKIDAN:
Funtzio batek sarreraren bat hartzen du eta emaitza bakar itzultzen du. Dagoeneko funtzio estandar hauek erabili ditut:

abs
arctan
arcsin (math unitatea beharrezkoa da)
arccos (math unitatea beharrezkoa da)
sin eta cos
sqrt
round, trunc, frac eta int

ZER IKASIKO DUDAN:
Funtzioekin jarraituz random funtzio estandarra ikasiko dut eta hori erabiltzeko randomize prozedura estandarra ikasiko dut. Funtzioekin jarraituz, ln eta exp funtzio estandarrak ikasiko ditut ere. Bide batez, datuak teklatuz emateko readln prozedura erabiliko dut.

Zerrenda honetan azpiprograma estandar batzuk deskribatzen dira:

FUNCTION    ABS    ( Zenbakia : Integer | Real ) : Integer | Real ;
FUNCTION    SQR    ( Zenbakia : Integer | Real ) : Integer | Real ;
FUNCTION    SQRT   ( Zenbakia : Integer | Real ) : Real ;
FUNCTION    EXP    ( Zenbakia : Real ) : Real ;
FUNCTION    LN     ( Zenbakia : Real ) : Real ;
FUNCTION    SIN    ( Angelua : Real ) : Real ;
FUNCTION    COS    ( Angelua : Real ) : Real ; 
FUNCTION    ARCSIN ( Zenbakia : Real ) : Real ;
FUNCTION    ARCCOS ( Zenbakia : Real ) : Real ;
FUNCTION    ARCTAN ( Tangentea : Real ) : Real ;
FUNCTION    ROUND  ( Zenbakia : Real ) : Integer ;
FUNCTION    TRUNC  ( Zenbakia : Real ) : Integer ;
FUNCTION    FRAC   ( Zenbakia : Real ) : Real ;
FUNCTION    INT    ( Zenbakia : Real ) : Real ;
FUNCTION    RANDOM ( Zenbakia : Integer ) : Integer ;
FUNCTION    RANDOM : Real ;
PROCEDURE   RANDOMIZE ;

Randomize eta Random(parametroa)

Dado bat 3 aldiz jaurti dela simulatuko dugu. Dadoak 6 posibilitate ditu: 1, 2, 3, 4, 5 eta 6. Gure programak 3 jaurtiketa aleatorien emaitzak batuko ditu eta baturaren arabera mezu hau pantailaratuko du:

3 jaurtiketen baturak 15 edo gehiago balio badu, pantailaraketa Oso ondo izango da
3 jaurtiketen batura 11 eta 14 artekoa bada, pantailaraketa Nahiko ondo izango da
3 jaurtiketen batura 6 eta 10 artekoa bada, pantailaraketa Txarto izango da
3 jaurtiketen baturak 5 edo gutxiago balio badu, pantailaraketa Oso txarto izango da

Randomize eta Random

Zenbaki errealekin lan eginez, balio aleatorioak lortzen dituen programa idatziko dugu.

Auto baten abiadura adierazten duen zenbaki erreal bat aleatorioki lortuko da, baina zenbaki aleatorio horren balioa bi mugen artekoa izan beharko da: behemuga 27.8 km/h eta goimuga 104.5 km/h.

Auto horren denbora adierazten duen zenbaki erreal bat aleatorioki lortuko da, eta bigarren zenbaki aleatorio horren balioa bi mugen artekoa izan beharko da ere: behemuga 0.8 segundo eta goimuga 2.0 segundo.

Eskatzen den programaren exekuzio-adibide bat jarraian erakusten da:

Ln eta Exp

5.2^x=7.9 bezalako ekuazio esponentziala ebazteko logaritmoa erabil behar da, hots, logaritmo nepertarra kalkulatzen duen ln funtzio estandarra. Modu beretsuan, 7.1^3.4=x bezalako ekuazioak ebazteko exp funtzio estandarra aplika dezakegu.

Eskatzen den programaren exekuzio-adibide bat ikusi:

Ln eta beste oinarriko logaritmoak

Zenbaki errealekin lan eginez, balio positibo bat teklatuz irakurri eta programak zenbakiaren logaritmo hamartarra kalkula dezala. Logaritmo hamatarra edo bitarra eskuratzeko funtzio estandarrik ez dagoenez, logaritmo nepertarraren funtzioa aplikatu beharko da formula hauen arabera:

log₁₀(x) = ln(x)/ln(10)

log₂(x) = ln(x)/ln(2)

Exp eta beste oinarriko potentziak

Zenbaki errealekin lan eginez, balio positibo edo negatibo bat teklatuz irakurri (adibidez 7.1) eta programak zenbakiaren 10-eko potentzia kalkula dezala (emaitza x=10^7.1). Horrelako lana burutzeko funtzio estandarrik ez dagoenez, logaritmo nepertarraren funzioa eta e zenbakiari dagokion potentziaren funtzioa aplikatu beharko dira esleipen hau eginez:

ln(rEmaitza) := rZenbakia*ln(10);
rEmaitza := exp(rZenbakia*ln(10));

Goiko esleipenaren justifikazioa jarraian ematen da:

            Z datua den zenbaki erreala
            X lortu nahi den potentzia

            X = 10^Z   logaritmo hamartarrrak hartuz:
                       log(X) = log(10^Z)  --->  log(X) = Z·log(10) 
                       log(X) = Z·log(10)  --->  log(X) = Z·1
                       ln(X)/Ln(10) = Z·1  --->  ln(X) = Z·ln(10)
            ln(X) = Z·ln(10)   exp funtzioa aplikatuz:
                               ln(X) = Z·ln(10) 
                               exp(ln(X)) = exp(Z·ln(10))
                               X = exp(Z·ln(10))

ArcSin eta ArcCos

Zenbaki errealekin lan eginez, angelu baten sinua adierazten duen balio bat teklatuz irakurri (-1.0 eta +1.0 arteko balioa) eta programak angelua lortuko du radianetan:

rAngelua := arcsin(rSinuarenDatua);

Gauza bera egin daiteke datua angeluaren kosinua baldin bada arccos funtzioa aplikatuz. Edozein kasutan, arcsin eta arccos funtzio estandarrak erabil ahal izateko math unitatea kargatu beharko da (arctan funtzioak ez du math unitearen beharrik).

Hemen arcsin funtzioaren grafikoa (irudiaren gainean klik egin balioak emateko):

Hauxe izan daiteke eskatzen den programaren irteera:

Orriak

2024(e)ko otsailaren 28(a), asteazkena

2024(e)ko otsailaren 17(a), larunbata

2024(e)ko otsailaren 8(a), osteguna